ASTM A106 管線彎徑比分析報告：針對 R/D= 1.5, 3.0, 5.0 進行結構完整性、流體效率與規範遵循的比較研究 (ASTM A106 Piping Bend Radius Ratio Analysis Report: Comparative Study of Structural Integrity, Fluid Efficiency, and Code Compliance for R/D = 1.5, 3.0, and 5.0)

一、基礎材料與幾何定義

 

1.1. ASTM A106 規範及其高溫運作的背景

ASTM A106/ASME SA106 規範涵蓋無縫碳鋼公稱壁厚管線，專為高溫高壓流體和氣體輸送而設計，廣泛應用於石油和天然氣煉製廠、發電廠、石化廠、鍋爐和船舶等關鍵工業環境中 ¹。該材料的選擇至關重要，因為無縫結構消除了沿管線長度方向的縱向銲縫，這些銲縫在高應力或高疲勞應用中往往是潛在的失效點。

從機械性能來看，ASTM A106 材料，特別是常用的 Grade B 和 Grade C，提供了高強度和足夠的延展性以應對高壓環境和成形操作 ²。例如，Grade B 規定最小屈服強度為 240 MPa，最小抗拉強度為 415  MPa；而 Grade C 則更強，最小屈服強度為 275  MPa，最小抗拉強度為 485 MPa ²。這種固有的韌性和強度是成功進行彎曲操作的先決條件，特別是對於彎曲半徑較小的幾何形狀。

規範明確指出 A106 管線適用於「彎曲、翻邊及類似成形操作」 ¹。這確立了該材料在遭受彎曲過程中，局部壁厚變化（變薄/變厚）和截面變形（橢圓化）的結構行為是設計分析的重點。在高壓代碼（如 ASME B31.3）的應用中，由於 A106 材料本身的優異性能，結構設計約束主要從材料本身的靜態失效轉移到由幾何形狀引起的局部應力集中和流體動力學效率。

 

1.2. 彎曲運動學與 R/D 比例分類

彎徑比 (R/D) 定義為彎曲中心線半徑 (R) 與管線公稱外徑 (D) 之比。這個比率是決定彎曲組件結構和流體行為的單一最重要的幾何參數。本報告分析的三種 R/D 比例代表了工業管線設計中的三個關鍵設計點：

1. R/D=1.5 (標準長半徑彎頭): 該比例是工業上最常見的標準對銲彎頭配件（長半徑彎頭，LR Elbow）⁴。它在節省空間和流動效率之間提供了一個標準化的平衡點，且作為標準件易於獲取和安裝 ⁶。
2. R/D=3.0 (中等半徑定製管彎): 該比例通常超出 ASME B16.9 標準配件的範圍，需要通過定製彎曲工法（熱彎或冷彎）由直管段製成 ⁸。在有限元分析 (FEA) 和實驗研究中，R/D=3.0 經常被用作平穩彎曲的基準點 ⁸。
3. R/D=5.0 (大半徑定製管彎): 該比例代表了一種趨向於非常平緩、大半徑管線彎曲的設計，旨在最大限度地優化流體流動並最小化結構應力 ⁹。

從工程角度來看，從 R/D=1.5（標準化、成本可預測）過渡到 R/D=3.0 或 R/D=5.0（定製彎曲件）涉及顯著的成本和時間安排差異。定製彎曲件必須滿足更嚴格的製造後壁厚要求（根據 ASME B31.3），這要求製造過程必須有精確的控制和驗證 ¹¹。在設計決策中，如果設計師選擇 R/D≧3.0，則必須將彎曲過程中的公差控制（例如，針對薄壁使用芯軸，以防止起皺或壓扁）⁴ 和較高的初始直管段材料成本納入考量。

 

1.3. 製造考量與質量控制

大半徑管線彎曲件（R/D≧3.0）通常通過冷彎（有時稱為現場彎曲，用於管線建造）或熱彎製造 ⁴。熱彎通過加熱降低了成形所需的力量，但可能導致材料局部性能變化；冷彎則依賴純粹的機械力，並且對於需要防止壓扁或橢圓化的薄壁材料，通常需要使用內部芯軸 ⁴。

製造彎曲件時的主要關注點是保持壁厚（特別是外徑處的變薄）和最小化截面變形（橢圓化）⁴。 ASTM A106 規範本身對 NPS 2 及以下的管線規定了冷彎測試，強調了成形品質的重要性 ¹。

彎曲半徑與製造可行性和成本之間存在固有的關係。雖然 R/D=1.5 彎頭是標準產品，但定製製造 R/D=3.0 或 R/D=5.0 的管線彎曲件，由於其曲率更平緩，通常更容易執行且固有缺陷（如壓扁）風險較低 ⁴。然而，這兩種較大半徑的彎曲件需要更大的物理空間進行製造和安裝。對於 R/D=1.5 這種緊密彎曲，如果壁厚較薄，其製造缺陷（例如，波紋、壓扁或塌陷）的風險會顯著增加 ⁴。由於 R/D=5.0 的曲率最淺，即使整體佔用面積大，其在製造過程中由局部應變集中引起的缺陷風險也最低。

 

二、結構完整性與應力分析

 

2.1. 理論基礎：柔性與截面橢圓化

管線彎曲件的機械行為與相同截面的直管段顯著不同。它們具有更高的柔性，並且伴隨著比直管高得多的局部應力和應變，主要特徵是截面變形，即「橢圓化」 ⁸。

橢圓化機制

當管彎承受平面內彎矩（閉合或張開彎矩）時，其圓形截面傾向於變形成橢圓形，即沿彎曲平面垂直方向扁平化 ⁸。這種橢圓化導致應力從膜應力重新分配到彎曲應力分量，從而放大最大應力 ¹³。這種截面變形的程度和應力放大與彎曲幾何參數 λ（或h）密切相關。相較於較大半徑的 R/D=5.0 彎曲件，較緊密的 R/D=1.5 彎曲件會產生更大的橢圓化 ⁸。

在高壓 A106 系統中，內部壓力在結構行為中扮演了關鍵角色。內部壓力傾向於抵抗和限制管彎的橢圓化 ⁸，從而對管彎起到硬化作用。因此，在高壓操作條件下計算出的實際柔性因子和應力強化因子（SIF）將低於零壓力條件下的計算值 ¹⁴。這種壓力硬化效應對於柔性最大、應力集中潛力最高的緊密彎曲 (R/D=1.5) 來說，其結構邊際效益是最大的，相比之下，對於本質上較硬的 R/D=5.0 彎曲件，效益則不那麼顯著。

 

2.2. 應力強化因子 (SIF) 與柔性因子 (k) 的定量比較

管線規範（例如 ASME B31）採用應力強化因子 (SIF, i) 和柔性因子 (k) 來量化彎曲件相對於直管段的疲勞壽命和柔性 ¹⁵。這些因子主要由柔性特性參數 h 決定。對於平滑彎頭，參數 h 定義為 h = t R₁ / r₂²，其中 t 是公稱壁厚，R₁ 是彎曲半徑，r₂ 是管線平均半徑 ¹⁴。

SIF 和 k 與 h 呈反比關係：SIF (i) 為 i = 0.9/h^2/3，柔性因子 (k) 為 k = 1.52/h^{5/6 14}。這意味著 R/D 比例的變化對結構響應具有強烈的非線性影響。

隨著 R/D 比例的增加（假設 t/D 保持不變），參數 h 隨之增加。參數 h 的增加導致 SIF 顯著降低 ¹⁶，證明 R/D=1.5 彎頭在承受相同彎矩時，其局部峰值應力遠高於 R/D=5.0 彎曲件 ¹⁸。與此相反，柔性因子 k 隨著 R/D 比例的增加而增加。 R/D=5.0 彎曲件展現出最高的柔性，這使其在吸收管線系統中的熱膨脹位移方面最為有效 ¹⁹。

 

表 2.2.1：機械因子對彎徑比 (R/D) 的依賴性

參數	公式對 R1​ 的依賴性	R/D=1.5 (緊密)	R/D=3.0 (中等)	R/D=5.0 (平緩)
柔性特性參數 (h)	與 R1 成正比	最低 h	中等 h	最高 h
應力強化因子 (SIF, i)	與 h-2/3 成反比 14	最高 SIF	中等 SIF	最低 SIF
柔性因子 (k)	與 h-5/6 成反比 14	最低 k (最硬)	中等 k	最高 k (最柔)

由於 SIF 與 h 的 -2/3 次方相關，結構風險的降低並非線性。從 R/D=1.5 轉變到 R/D=3.0 所帶來的 SIF 降低和疲勞壽命改善是最為顯著的結構性能提升。此後，從 R/D=3.0 增加到 R/D=5.0 所帶來的額外安全邊際效益會遞減，而此操作將顯著增加系統佈局所需的空間 ¹⁷。因此，對於尋求減輕高週次熱應力的工程師來說，R/D=3.0提供了一個極佳的平衡點，能在不造成極端空間限制的情況下，實現大部分優化 R/D=5.0 所能提供的 SIF 降低效益。

 

2.3. 失效模式：疲勞與塌陷抗性

對於用於高溫高壓服務的 A106 管線，特別是在發電廠或煉油廠等頻繁啟動/停機的環境中 ¹，疲勞失效是一個至關重要的設計考慮因素。疲勞損傷通常在週期性平面內彎曲作用下，始於彎頭的側翼（flank）⁸。高 SIF 的組件 (R/D=1.5) 由於應力集中程度高，固有地更容易發生疲勞開裂 ²¹。

靜態載荷下的失效模式包括整體塑性變形和增量塑性塌陷（棘輪效應）²¹。組件對這些模式的抵抗力取決於彎曲幾何形狀和直徑壁厚比 (D/t)。有限元分析的極限載荷分析結果表明，線性彈性的 ASME 規範標準在預測實際塌陷強度方面可能過於保守 ¹²。

在三種幾何形狀中，R/D=5.0 具有最低的 SIF，因此在熱疲勞方面具有最高的抵抗力。相比之下，R/D=1.5 由於其極高的應力集中峰值，需要最高的疲勞分析安全裕度，並對材料質量控制提出最嚴格的要求 ¹⁸。

 

三、規範遵循與製造效應 (ASME B31.3)

 

3.1. 彎曲過程中的壁厚變化

當直管被彎曲時，內彎半徑（intrados）側的材料受到壓縮並增厚，而外彎半徑（extrados）側的材料被拉伸並變薄 ¹²。這種局部壁厚的變化是對彎曲件進行結構完整性評估的基礎。

關鍵的外徑變薄

結構完整性的檢查標準是彎曲後外徑處的最小剩餘壁厚 (t_extrados)，該厚度必須大於所需的壓力設計厚度 (t) 加上腐蝕餘量 (c) ¹¹。事實上，規範承認，即使一開始的管線具有滿足壓力設計要求的均勻厚度，彎曲操作後的外徑變薄也可能導致其不符合要求 ¹²。

 

3.2. ASME B31.3 最小所需壁厚計算

ASME B31.3 規範要求對彎曲管線使用修正的壁厚計算公式，該公式包含一個幾何因子 I，用於調整環向應力 ⁷。一般所需壓力設計厚度公式如下：

t = PD/2

其中，P 為內部壓力，D 為外徑，S 為許用應力，E 為質量係數，W 為銲縫強度因子，Y 為係數。因子 I 取決於彎曲半徑和所在位置（內徑或外徑）¹⁶。

因子 I 對 R/D 的依賴性 因子 I 定量地描述了彎曲管件的環向應力與相同尺寸直管段的差異：

• 內徑因子 I_i： I_i = [4 (R₁/D)–1]/ [4 (R₁/D)-2] ²²。此因子始終大於1.0，反映材料增厚導致的環向應力降低，從而降低了所需的設計壁厚。
• 外徑因子 I_e： I_e = [4 (R₁/D)+1]/ [4 (R₁/D)+2] ²²。此因子始終小於1.0，反映材料變薄導致的環向應力增加，從而要求更高的最小設計壁厚。

因子  I_e 越小，表示環向應力集中程度越高，要求在彎曲操作後必須保持越厚的壁厚才能滿足壓力設計要求。 R/D 比例對此因子的影響極大。

 

表 3.2.1：不同 R/D比例下的 I 因子與變薄剖面 (ASME B31.3)

彎徑比 (R​/D)	內徑 Ii​ 因子	外徑 Ie​ 因子	Ie​ 相對值 (1.0 = 直管)	外徑變薄風險
1.5	1.250	0.875	最低 (最偏離直管)	最高 (必須有最大補償)
3.0	1.100	0.929	中等	中等
5.0	1.056	0.955	最高 (最接近直管)	最低

註：I_e 和 I_i 因子值為基於 ASME B31.3 公式計算的精確分數近似值，反映了彎曲操作對環向應力的影響。

 

3.3. 初始壁厚選擇與成本影響

為了確保在最關鍵的外徑處（發生變薄的位置）保持最小所需厚度 (t_min)，設計師必須計算在彎曲之前所需的直管公稱壁厚，以計入預期的厚度損失 ¹¹。

R/D=1.5 彎曲件由於其 I_e 值最低 (0.875)，意味著它必須在彎曲操作中承受最嚴重的變薄。這迫使設計師必須選擇比連接直管段所需壓力設計厚度更高的初始 A106 公稱壁厚（通常是更高的管線表號），以補償損失 ²²。這直接導致更高的初始材料採購成本。

相比之下，對於 R/D=5.0 彎曲件，其 I_e 值 (≒0.955) 非常接近 1.0，因此所需的初始壁厚僅略高於連接直管段。從製造和材料經濟性來看，大半徑彎曲件的風險和成本補償要求最低。

 

四、流體動力學與水力性能

 

4.1. 彎曲管線中的流動阻力基礎

當流體被迫繞過彎曲管線時，流體慣性會產生二次流動模式（稱為迪恩渦流，Dean Vortices），這種現象產生了高度的湍流混合和邊界摩擦剪切應力，最終導致不可逆的壓力損失（水頭損失 h_f) ⁵。

水頭損失通常使用 Darcy-Weisbach 方程與阻力係數 (K) 結合來量化，其中 h_f = K_v² / 2g ²⁴。在 A106 管線系統典型的高流速應用中，流體通常處於湍流狀態（雷諾數 Re > 3000），因此摩擦因子和 K 值的準確確定至關重要 ²³。

 

4.2. 壓力降 (K 因子) 的比較分析

彎徑比對流體動力學性能具有直接影響。較緊密的彎曲 (R/D=1.5) 會產生更高程度的湍流和更大的壓力降，而較大半徑的彎曲 (R/D=5.0) 則提供更平穩的過渡 ⁵。

經驗數據表明，阻力係數 K 隨著 R/D 比例的增加而顯著下降 ²⁵。這種下降是系統流動效率的直接體現：

• R/D=1.5: 接近 r/d=1 的值，導致高損失係數（例如，對於某些尺寸/流動，90 度彎曲的 K≒0.5）²⁵。這類彎頭提供了快速、急劇的轉彎，但代價是更高的摩擦和壓力損失 ⁵。
• R/D=3.0: 顯示出可觀的損失減少，趨於穩定在最小有效損失值附近（例如，K≒0.3）²⁵。
• R/D=5.0: 提供了接近最佳的、最小的壓力損失。研究表明，將 R/D 進一步增加到約 5 或 6 以上時，彎曲係數的額外降低效益會變得微乎其微 ⁹。

從 R/D=1.5 標準彎頭過渡到 R/D=3.0 定製彎曲件，即可實現最顯著的水力性能提升（壓力降減少）。相比之下，從 R/D=3.0 到 R/D=5.0 的邊際收益在經濟上較難證明其合理性，除非管線設計的首要目標是極致的泵浦功耗最小化或嚴格的流體動力學平穩性。

 

表 4.2.1：水力阻力係數 (K) 比較 (90度彎曲)

彎徑比 (R/D)	幾何類型	阻力係數 (K90°​) 指標	壓力降幅度 (相對)	流動效率概況
1.5	標準 LR 彎頭	高 (指標: 1.0) 25	最高的湍流/損失	標準/可接受
3.0	定製管彎	中等 (指標: ≒0.6) 25	顯著降低	改善/高
5.0	大半徑管彎	最低 (指標: ≒0.5) 9	接近最小可能損失	最佳

 

4.3. 侵蝕與流動加速腐蝕 (FAC)

流動加速腐蝕 (FAC) 是碳鋼管線（如 A106）中的主要退化機制，尤其是在濕蒸汽或兩相流體環境中，導致局部壁厚變薄 ¹²。

R/D 比例對 FAC 風險有直接影響。緊密彎曲 (R/D=1.5) 在內徑處產生更高的局部壁面剪切應力和速度，加劇了侵蝕和腐蝕 ²⁷。這種湍流模式同樣影響了局部變薄率 ¹²。相比之下，較大的半徑 (R/D=5.0) 使流動剖面更加平滑，最大限度地減少了局部速度尖峰，從而降低了 FAC/侵蝕損壞的風險 ⁵。

這揭示了一個重要的結構與流體動力學的交互作用：雖然製造過程導致外徑機械變薄，但 FAC 傾向於攻擊高湍流區域，通常包括內徑和下游截面。因此，R/D=1.5 彎頭將高機械應變集中與更高的侵蝕/腐蝕率結合在一起，對長期可靠性提出了雙重挑戰。在需要高可靠性和長生命週期的高溫高壓 A106 應用中，採用 R/D≧3.0 的幾何形狀是降低這些耦合風險的關鍵策略。

 

五、設計權衡與建議

 

5.1. 綜合設計矩陣：性能權衡的綜合

本分析旨在為設計師提供一個集成參考，以便在結構完整性、規範遵循和流體動力學之間做出明智的選擇。這三種 R/D 比例各有優勢和劣勢，必須根據管線系統的具體運行要求進行評估。

表 5.1.1：ASTM A106 彎曲件的綜合性能比較

設計指標	R/D=1.5 (標準 LR 彎頭)	R/D=3.0 (定製彎曲件)	R/D=5.0 (大半徑彎曲件)
空間要求	最低 (緊湊)	中等 (需約 2 倍於 1.5D 的空間)	最高 (最大佈局佔地面積)
可得性/成本	標準配件 (最低單位成本)	定製製造 (較高成本，較長交期)	定製製造 (最高材料用量，最高成本)
應力強化因子 (SIF)	最高 (最高結構疲勞風險)	中等/低 (較 1.5D 顯著降低)	最低 (最佳結構性能)
柔性因子 (k)	最低 (最硬的組件)	中等	最高 (最利於熱位移吸收)
外徑變薄 (ASME Ie 因子)	最嚴重變薄 (Ie=0.875)	中等變薄 (Ie≒0.929)	最輕微變薄 (Ie≒0.955)
水力損失 (K 因子)	最高壓力降/湍流	中等損失 (優秀的平衡)	最低壓力降 (最佳流動)
侵蝕/FAC 風險	最高風險	中等/低風險	最低風險

 

5.2. 應用原則與工程選型指導

在設計高壓 A106 管線系統時，應將 R/D=1.5 視為在空間或成本受限時的權宜之計，而 R/D≧ 3.0 則應作為結構和水力學優化的預設標準。定製製造 R/D=3.0 彎曲件的額外成本通常在高可靠性系統的整個生命週期內是值得的，因為它可以顯著降低與疲勞和流動效率低下相關的營運成本。

 

選擇 R/D=1.5 的標準：

• 空間限制主導： 當廠房佈局嚴格限制管線體積時的首選。
• 低週期性服務或靜態載荷： 適用於連續運行且熱膨脹週期極少的系統。在此類系統中，初始成本和空間節約優先於長期疲勞性能。
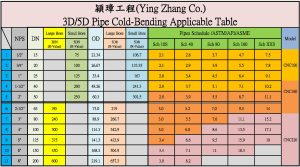
• 小直徑管線： 對於 NPS ≦2 的小公稱尺寸，標準彎曲規範通常限制了最小半徑的選擇 ¹。

 

選擇 R/D=3.0 的標準：

• 平衡設計： 在不承擔 R/D=5.0 帶來的極大空間懲罰的情況下，尋求流動效率和結構完整性（降低 SIF、延長疲勞壽命）顯著改善時的最佳解決方案。
• 標準週期性服務： 強烈推薦用於暴露於頻繁熱循環的關鍵高壓 A106 管線（例如，ASME 服務限制 Level B 和 C）。 R/D=3.0 提供了比 R/D=1.5 高得多的抗疲勞能力，同時仍保持合理的佔地面積。

 

選擇 R/D=5.0 的標準：

• 流動/侵蝕關鍵系統： 適用於最大限度地減少不可逆壓力降（例如，長距離管線、泵浦吸入管線）或必須減輕侵蝕/FAC 的系統。
• 高熱位移需求： 當需要最大柔性來吸收最大的熱位移時的選擇（k 因子效益最大）。

 

六、結論與建議

 

對於 ASTM A106 高壓無縫管線的應用，彎徑比 R/D 在 1.5、3.0 和 5.0 之間的選擇需要在空間、成本、結構可靠性和水力效率之間進行細緻的權衡。

1. 結構與疲勞性能優先： 彎徑比是決定管線疲勞壽命的應力強化因子 (SIF) 的主要驅動因素。 R/D=1.5 彎頭由於其最高的 SIF 和最強烈的橢圓化傾向，在週期性載荷下對疲勞失效的敏感性最高。向 R/D=3.0 的轉變提供了最大的結構安全邊際收益，因為 SIF 隨 h 的 -2/3 次方快速下降。在高壓系統中，操作壓力對橢圓化的抑制作用對最脆弱的 R/D=1.5 彎頭提供了非線性的最大硬化效益。
2. 規範遵循與成本控制： 根據 ASME B31.3 規範，緊密彎曲 (R/D=1.5) 導致外徑變薄最嚴重 (I_e=0.875)，這要求設計師必須從比連接直管段所需壁厚高得多的初始管線厚度（即更高的管線表號）開始進行製造，以確保最小壁厚要求得到滿足。這會顯著增加 R/D=1.5 的材料成本。相反，R/D=5.0 的變薄影響最小，從而最大限度地降低了製造風險和額外的材料要求。
3. 水力學與營運效率： 壓力損失 (K 因子) 隨 R/D 的增加而減少。 R/D=3.0 彎曲件在水力性能上提供了比 R/D=1.5 彎頭顯著的改善，有效降低了湍流、泵浦功耗和潛在的 FAC/侵蝕風險。從 R/D=3.0 到 R/D=5.0 的性能提升雖然存在，但在經濟上通常難以證明其合理性，除非流動效率是絕對的首要任務。

建議： 鑑於 ASTM A106 管線的應用性質（高溫高壓、關鍵系統），除非空間限制絕對嚴格，否則應避免使用 R/D=1.5 作為默認選擇。R/D=3.0 的定製彎曲件通常是最佳的工程解決方案。它在結構完整性（較低的 SIF）、水力效率（較低的 K 因子）和安裝空間要求之間實現了最優異的平衡，為長期運行可靠性和成本效益提供了卓越的表現。

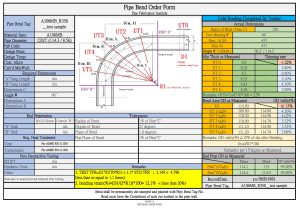
(照片分享:A106B_OD114.3-8.56t  5.0D冷作彎管花絮)

參考文獻

1. ASTM A106 Pipe Specifications | American Piping Products, https://amerpipe.com/products/carbon-pipe/a106/a106-specifications/
2. ASTM A106 Grade B Pipe Specification – Octal Steel, https://www.octalsteel.com/astm-a106-grade-b-pipe/
3. ASTM SA/A106 Seamless Steel Pipe Specifications – Federal Steel Supply, https://www.fedsteel.com/products/carbon-pipe-and-tube/astm-a106/
4. Pipe Bends: A Quick Primer – Unified Alloys, https://www.unifiedalloys.com/blog/pipe-bends
5. Short Radius Elbow vs Long Radius Elbow: Understanding the Differences – Piyush-Steel, https://www.piyush-steel.com/blog/short-radius-elbow-vs-long-radius-elbow-understanding-the-differences/
6. Long Radius vs Short Radius Elbows: Key Differences Explained – United Forge, https://www.unitedforgeind.com/blog/long-radius-vs-short-radius-elbows/
7. Piping and Pipeline Bends – EPCM Holdings, https://epcmholdings.com/piping-and-pipeline-bends/
8. Mechanical Behavior of Steel Pipe Bends; An Overview. – University of Edinburgh Research Explorer, https://www.research.ed.ac.uk/files/29451682/PVP_15_1165.pdf
9. Pressure losses for fluid flow in 90 degrees pipe bends, https://nvlpubs.nist.gov/nistpubs/jres/21/jresv21n1p1_A1b.pdf
10. Comparison between twice the maximum shear stress calculated from Code… – ResearchGate, https://www.researchgate.net/figure/Comparison-between-twice-the-maximum-shear-stress-calculated-from-Code-and-those-from-FEA_fig2_309914137
11. ASME B31.3 Pipe Bend Calculators – Pipeng Toolbox, http://pipeng.com/index.php/ts/itdmotdiam002l/
12. DETAILED FEA OF LOCALLY THINNED PIPE BENDS – NC State Repository, https://repository.lib.ncsu.edu/bitstreams/35ce44b7-fa82-49d9-ab60-6e1db09f931b/download
13. – Propagation of ovalization a long straight pipes and elbows MILLARD A., ROCHE R. – INIS-IAEA, https://inis.iaea.org/collection/NCLCollectionStore/_Public/13/675/13675704.pdf
14. SIF3 | PDF | Pipe (Fluid Conveyance) | Radius – Scribd, https://www.scribd.com/document/887530207/SIF3
15. ASME B31.3 Process Piping – AquaEnergy Expo Knowledge Hub, https://kh.aquaenergyexpo.com/wp-content/uploads/2025/02/ASME-B31.3-Process-Piping.pdf
16. “INDUCTION BENDS 100103–TM–001–REV 2 – Stressman Engineering AS, https://stressman.no/wp-content/uploads/2020/12/100103-TM-001-Rev-2-LR.pdf
17. Analysis of Elbow Stress Intensification Factors for Piping System – Clausius Scientific Press, https://www.clausiuspress.com/assets/default/article/2022/11/22/article_1669126504.pdf
18. Finite Element Analysis of the Mechanical Behavior of Mitered Steel Pipe Elbows under Bending and Pressure, https://www.nwpipe.com/app/uploads/2020/08/Spyros-Mitered-Elbows-Seiesmic-Analysis.pdf
19. E6/5 Plastic Instability Test of Elbows Under In-Plane and Out-of-Plane Bending – NC State Repository, https://repository.lib.ncsu.edu/bitstreams/db402f81-3008-4516-94d4-132a1d3e1834/download
20. (PDF) Mechanical Behavior of Steel Pipe Bends: An Overview – ResearchGate, https://www.researchgate.net/publication/283849663_Mechanical_Behavior_of_Steel_Pipe_Bends_An_Overview
21. Plastic collapse of elbows under combined internal pressure and in-plane bending | Request PDF – ResearchGate, https://www.researchgate.net/publication/223310380_Plastic_collapse_of_elbows_under_combined_internal_pressure_and_in-plane_bending
22. Calculation As Per Asme b31.3 | PDF | Pipe (Fluid Conveyance) | Plumbing – Scribd, https://www.scribd.com/document/410660149/Calculation-as-Per-Asme-b31-3
23. Pipeline Pressure Loss – Fluid Mechanics Ltd, https://www.fluidmechanics.co.uk/hydraulic-calculations/friction-in-pipes-and-passages/
24. Bend Loss Model – Documentation, https://docs.aft.com/fathom/BendLossModel.html
25. Some Friction Loss Tables – Plumbing Supply, https://www.plumbingsupply.com/ed-frictionlosses.html
26. Darcy–Weisbach equation – Wikipedia, https://en.wikipedia.org/wiki/Darcy%E2%80%93Weisbach_equation
27. Computational Fluid Dynamic Simulations of Pipe Elbow Flow – OSTI.GOV, https://www.osti.gov/servlets/purl/919140